Chapter Four: Synthesis

Variations in FM Synthesis

Many approaches can produce more complex spectra with FM. The Yamaha DX7 synthesizer popularized the idea of double-carrier FM, in which a single modulator controls two carriers tuned differently. This allows the creation of formant areas not achievable with single-carrier FM. It also employs stacks of modulators in series, where a modulator was itself modulated, which could either produce wildly complex spectra if tuned inharmonically or produce weighted spectra that emphasize lower partials for more realistic bass. This addresses one of FM’s drawbacks—the upper and lower sidebands have equal strength—while human hearing requires more low-frequency energy to be perceived as equally loud. As a result, single-carrier FM can sound treble-heavy, especially at higher modulation index (I) settings. Another interesting idea for producing more complex sounds is to modulate the modulation index itself, providing a rapid timbral shift, or to low-frequency-modulate the modulator or carrier, changing the C:M ratio and thus the sideband frequencies for striking effects.

Suggested Listening Examples

To hear audio-rate FM used with a high level of artistry, there can be no better source than the works of John Chowning himself. Highly recommended are Stria (1976), Turenas (1972) and Phoné (1981). Barry Truax was another pioneering FM composer with Arras, Androgyny, Wave Edge, Solar Ellipse, and Sonic Landscape No. 3.

The concept of the normal form for a C:M ratio has been used for a long time. It helps predict which ratios yield the same set of sideband frequencies, though it does not predict their relative strengths or phases. If the value of M in a ratio is less than twice the value of C, it is not in normal form, but can be reduced to normal form by applying the operation: C = |C - M|. What this means is that you subtract M from C (ignoring any minus sign) and treat the result as the new C value. You keep doing this (often several times) until the ratio satisfies the normal form criterion.

For example, take the C:M ratio of 3:2. Take 3 - 2 and get 1. That is the new value of C (keep the old value of M), so the new ratio will be 1:2. How is this possible—how can 3:2 produce the same sidebands as 1:2? Let's try it out with 300:200 Hz as our 3:2 ratio and 100:200 Hz as our 1:2 ratio.

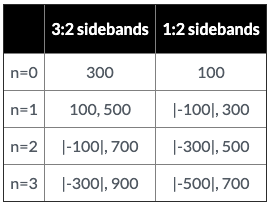
You can see they produce the same frequencies, but with sidebands of different orders and different reflections. Therefore, the way these frequencies react to changing values of I will be completely different. But some interesting things can be deduced using normal form. A C:M ratio is in normal form when the carrier is the fundamental in the spectrum it produces, as in our 1:2 example above—100 Hz is the fundamental. Harmonic normal form ratios are always of the type 1:N where N is an integer, and inharmonic ones are not. For a much more detailed treatment of normal form, visit Barry Truax's FM theory page.

Suggested FM Theory Reading

Chowning, John M. “The Synthesis of Complex Audio Spectra by Means of Frequency Modulation.” Journal of the Audio Engineering Society 21, no. 7 (1973). Reprinted in Computer Music Journal 1, no. 2 (1977); and in Foundations of Computer Music, ed. Curtis Roads and John Strawn (Cambridge, MA: MIT Press, 1985).

Truax, Barry. “Organizational Techniques for C:M Ratios in Frequency Modulation.” Computer Music Journal 1, no. 4 (1978): 39–45. Reprinted in Foundations of Computer Music, ed. Curtis Roads and John Strawn (Cambridge, MA: MIT Press, 1985).

Dodge, Charles, and Thomas A. Jerse. Computer Music. 2nd ed. New York: Schirmer, 1997.

Moore, F. Richard. Elements of Computer Music. Englewood Cliffs, NJ: Prentice Hall, 1990.